اصول فیزیکی فصل1

اصول علمی و کاربردی

بیومکانیک در ارتودنسی

مترجم: دکتر عبدالرضا جمیلیان

متخصص ارتودنسی و فلوشیپ ارتودنسی جراحی و سندروم های فک و صورت

دانلود در انتهای فصل

دانشیار بخش ارتودنسی وعضو مرکز کرانیوفیشیال واحد دندانپزشکی دانشگاه آزاد اسلامی

انتشارات: آرتین طب

محتویات

مقدمه

1. اصول فیزیکی

2. کاربرد نیروی ارتودنتیک

3. آنالیز مکانیک‌های بین دو دندان

4. سیستم های دارای اصطکاک و بدون اصطکاک

5. کنترل انکوریج

6. تصحیح ناهنجاریهای عمودی

7. تصحیح ناهنجاریهای عرضی

8. تصحیح ناهنجاری‌های قدامی خلقی

9. بستن فضا

فرهنگ لغات

ضمیمه

مقدمه

به محض کامل شدن تشخیص و طرح درمان نوع دستگاه ارتودنسی و سیستم مورد نظر برای رسیدن به اهداف درمانی می‌بایست طراحی گردد. کاربرد صحیح اصول بیومکانیک به انتخاب دستگاه مناسب کمک می نماید.

در خلال سه دهه اخیر پیشرفت‌های قابل توجهی در زمینه تکنولوژی ارتودنسی به عمل آمده است. مواد جدید در ساخت و طراحی براکت‌ها، باندینگ و سیم‌های ارتودنسی باعث شده است که امکان ساخت دستگاه‌های مختلف ارتودنسی فراهم گردد. همچنانکه این مواد جدید وارد ارتودنسی می‌شود لازم است که اصول بیومکانیک برای یک طرح درمان موفق به طور کامل درک گردد. عدم شناخت اصول بیومکانیک نه تنها باعث ایجاد نیروهایی در جهت نامناسب می‌گردد بلکه به بافتها نیز صدمه می‌زند. بنابراین طرح درمان موفق نیاز به دانش بیومکانیک دارد.

این کتاب به منظور معرفی تکنولوژی، بررسی مواد مورد استفاده در ارتودنسی و اصول بیومکانیک در طراحی دستگاه‌های ارتودنسی نوشته شده است.

ناندا
بنام خداوند بخشنده مهربان

کتاب حاضر ترجمه جدیدترین نسخه ی Biomechanics in Orthodontics: Principles and Practice می باشد . با توجه به اهمیت موضوع بیومکانیک و استفاده ی درست از نیروها در درمانهای ارتودنسی ، این کتاب به همه دانشجویان و همکاران محترم تقدیم می شود .

امیدوارم این کتاب در ارتقاء سطح دانش دانشجویان و رزیدنتهای ارتودنسی تاثیر بسزایی داشته باشد و آنها را قادر سازد از مطالب آن در طرح درمانهای خود به بهترین نحو استفاده کنند .

لطفاً با ارائه نظرات و پیشنهادهای خود برای هرچه بهتر شدن کتاب در چاپ های بعدی جهت ارتباط با اینجانب به سایت اینترنتی WWW.Jamilian.net مراجعه ویا به آدرس Info@Jamilian.net مکاتبه نمایید .

دکترعبدالرضا جمیلیان

بهترین متخصص ارتودنسی و فلوشیپ ارتودنسی جراحی و سندروم های فک و صورت

دانشیار بخش ارتودنسی وعضو مرکز کرانیوفیشیال واحد دندانپزشکی دانشگاه آزاد اسلامی

به نام خداوند علم و خرد

مباحث بیومکانیک به عنوان اصول پایه برای حرکت دادن دندان در رشته ارتودنسی می باشد دانستن این اصول برای هر متخصص ارتودنسی جهت رسیدن به اهداف درمانی امری ضروری است و هر متخصص ارتودنسی می بایست از تمام جزئیات آن به طور کامل مطلع باشد .

اینجانب دکتر عبدالرحمن شوکت بخش به عنوان ارائه دهنده دروس ارتودنسی تکنیک عملی و بیومکانیک برای دانشجویان دوره تخصصی این افتخار را دارم که اعلام نمایم همکار عزیز جناب آقای دکتر عبدالرضا جمیلیان در کسوت عضو هیئت علمی به عنوان دانشیار بخش ارتودنسی مرکز علوم دندانپزشکی دانشگاه آزاد اسلامی کتاب اصول بیومکانیک ناندا را با ترجمه ای بسیار قابل درک و فهم و به شیوه ای روان انجام داده اند و این کتاب را در اختیار همکاران علاقه مند برای رسیدن به نتایج مطلوب درمانی و هم چنین برای دانشجویانی که وارد این رشته می شوند قرار داده است . کتابهای مرجع که به صورت آسان به زبان فارسی در اختیار علاقه مندان قرار می گیرد، می تواند در رسیدن به اهداف درمان موثر واقع شود . اینجانب تلاش وسعی آقای دکتر عبدالرضا جمیلیان در جهت ارتقاء حرفه و دانش ارتودنسی در ایران را قدردانی می نمایم و از خداوند بزرگ و متعال موفقیت و پیشگامی در این رشته را برای ایشان آرزومندم .

دکتر عبدالرحمن شوکت بخش

سرپرست دوره فلوشیپ ارتودنسی جراحی

دانشکده دندانپزشکی دانشگاه علوم پزشکی شهید بهشتی

فصل اول – اصول فیزیکی

حرکت دندان در درمانهای ارتودنسی نیاز به کاربرد نیرو و پاسخ بافت پرویودنتال به این نیروها دارد. اصول مکانیک توسط قوانین فیزیک همانند نیوتن (Newton) و هوک (Hook) کنترل می‌گردد. این فصل، تعاریف اساسی و اصول مکانیکی کاربردی را بحث می‌نماید که بستری برای فصول بعدی می‌باشد.

قوانین نیوتن

سه قانون نیوتن (1727-1642) که روابط بین نیرو و جسم و حرکات آنها را آنالیز می‌نماید در ارتودنسی کاربرد دارد.

قانون اینرسی

قانون اینرسی، ثبات اجسام را آنالیز می‌نماید. هر جسمی در سکون است و یا به حرکت خطی خود ادامه می‌دهد. مگر اینکه با نیروی دیگری مواجه شود.

قانون شتاب

قانون شتاب می‌گوید که تغییر در حرکت در رابطه با نیروی محرکی که به آن وارد میشود نسبی است. شتاب در جایی که نیرو وارد میشود در یک مسیر خطی، اتفاق می‌افتد.

M × F = A

شتاب = A

نیرو = F

جرم = M

قانون عمل و عکس العمل

عکس العمل دو جسم در برابر یک دیگر همیشه مساوی و در خلاف جهت می‌باشد. بنابراین در هر عملی یک عکس العمل برابر و در خلاف جهت وجود دارد.

بردارها

از اتصال دو نقطه یک خط حاصل میشود. وقتی از هر یک از نقاط به سوی نقطه دیگر حرکتی آغاز شود یک مسیر یا جهت ایجاد میشود. میزان نیرو که در یک نقطه بر روی جسم تاثیر می‌گذارد بردار نامیده میشود و توسط یک پیکان(Arrow) نشان داده می‌شود. برای مثال، در شکل 1-1 جهت نیرو که از طریقLabial Bow دستگاه متحرک بر روی سطح لیبیال انسیزورهای فک بالا اعمال می‌شود در مسیر افقی می‌باشد. جهت نیرو در مسیر خلفی اعمال می‌گردد (از سمت قدام به خلف) و طول پیکان میزان نیرو را نشان می دهد.

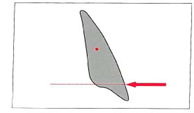
شکل 1-1. نیرو یک بردار است. نیرویی که بر روی دندان انسیزور اعمال می‌شود با طول پیکان نشان داده شده است. نیرو بر روی تاج دندان وارد میشود. جهت نیرو افقی است و مسیر آن از قدام به خلف است.

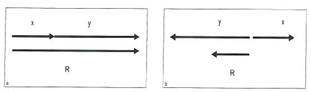
شکل 2-1. جمع 2 نیرو در یک خط و در یک مسیر برابر با جمع دو نیرو است. R=x+y شکل a و جمع 2 نیرو در یک خط و در 2 مسیر مخالف برابر با جمع جبری دو نیرو است. R=x+(-y) شکل b

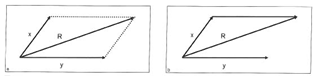
شکل 3-1.(a) برآیند نیرو (R) که از جمع 2 بردار y, x در یک مسیر حاصل می‌شود برابر با قطر متوازی الاضلاعی است که 2 بردار در دو سمت آن واقع است.(b). برآیند نیرو (R) همچنین می‌تواند با رسم یک بردار به موازات بردار y از انتهای بردار x شروع شود. سپس از انتهای این بردار به ابتدای بردار x وصل شود.

جمع بردارها

بردارها بر روی محور مختصات تعریف می‌شوند. برای بردارها وجود 2 محور مختصات کافی است. در شکل a2-1 مشاهده میشود که برآیند نیروهای مختلف y,x که در یک خط و در یک جهت هستند برابر با جمع دو بردار می‌باشد (x+y). برآیند دو بردار در یک خط اما در 2 مسیر مختلف برابر با جمع جبری دو بردار است. (x+[-y]) (شکل b2-1)

برآیند دو بردار که از یک نقطه جدا میشود برابر با قطر متوازی الاضلاعی است که دو بردار در دو سمت آن واقع است (شکل a3-1) همچنین، برآیند این بردار با اتصال یک بردار به موازات بردار y از انتهای بردار x شروع میشود. سپس انتهای این بردار به ابتدای بردار x وصل می‌گردد (شکل b 3-1).

جمع چند بردار

جمع چند بردار همانند جمع دو بردار محاسبه می‌شود. بنابراین بردار سوم با برآیند دو بردار اول و دوم جمع می‌گردد و همینطور برای بردارهای بیشتر محاسبه می‌گردد (شکل 4-1).

تفریق 2 بردار

به منظور تفریق دو بردار، بردار دیگری (-y) در مسیر مخالف از انتهای بردار x و به موازات بردار y کشیده می‌شود سپس از ابتدای بردار x به انتهای آن بردار وصل می‌شود (-y). بنابراین برآیند R از نقطه اثر نیرو در محل تلاقی x و y به سوی انتهای محور –y رسم می‌شود.

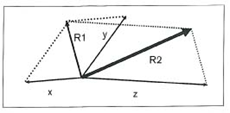
شکل 4-1. برای به دست آوردن برآیند چند بردار که دارای نقطه اثر یکسانی هستند. در ابتدا بر آیند R’ از بردار y , x کشیده می‌شود. سپس برآیند R2 از بردار Z و بردار R1 به دست می‌آید.

Z + R1 = R2 ،x + y =R1

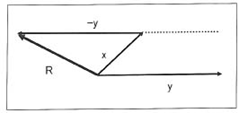
شکل 5-1. تفریق دو بردار که دارای یک نقطه اثر می‌باشند. توسط بردار دیگری (-y) که از انتهای بردار x کشیده می‌شود و به موازات بردار y و در خلاف جهت آن است به دست می‌آید سپس انتهای بردار –y به محل اتصال بردار y , x متصل می‌شود.

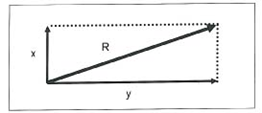
شکل 6-1. تجزیه برآیند نیرو به اجزاء تشکیل دهنده آن در یک محور مختصات با محورهای y , x.

تجزیه یک بردار به اجزاء آن

برای تجزیه یک بردار به اجزاء آن دو خط موازی از نقطه اثر برآیند به سمت اجزایی که ایجاد می‌کند، کشیده می‌شود. با کشیدن دو خط موازی از انتهای برآیند R به سوی خطوط ذکر شده یک متوازی الاضلاع حاصل می‌شود. جمع 2 مولفه ایی که از این طریق به دست می‌‌آید برابر با برآیند R است.

تجزیه برآیند به اجزاء تشکیل دهنده آن به منظور درک بهتر نیروها و به منظور محاسبات مثلثاتی توسط محورهای x و y نمایش داده می‌شود (شکل 6-1). در حقیقت برآیند می‌تواند در جهت‌های بسیار زیادی تجزیه شود. به طور معمول محور x در جهت افقی و محور y در جهت عمودی پذیرفته شده است.

نیرو

نیرویی که بر یک جسم وارد میشود باعث تغییر موقعیت و یا تغییر شکل جسم می‌شود. در ارتودنسی نیرو با گرم ، انس یا نیوتن اندازه گیری می‌شود. نیرو یک بردار است که دارای جهت، مقدار و نقطه اثر می‌باشد. در ارتودنسی عواملی مثل توزیع و مدت نیرو مهم هستند. در خلال حرکت Tippingنیرو در یک سمت در ناحیه کرست استخوان آلوئول و در سمت دیگر در ناحیه آپکس وارد میشود (شکل a7-1). در خلال حرکت انتقالی نیرو به صورت یکسان بر روی استخوان و سطح ریشه پخش می‌شود (شکل b 7-1).

مدت اثر نیرو

ثبات نیرو

بهترین نیرو، مقداری است که بدون آثار تخریبی بر روی بافت پریودنتال یا درد برای بیمار باعث سریعترین حرکت گردد. برای رسیدن به مطلوب ترین پاسخ بیولوژیکی در بافت پریودنتال، وجود نیروی کم و پیوسته (Light and Continuous) ضروری است. مقایسه کاهش نیرو در طول زمان در 2 نوع مختلف Coil Springبا نسبت load/deflection کم و زیاد در شکل 8-1 نشان داده شده است.

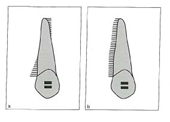
شکل 7-1. توزیع نیرو در استخوان آلوئول و سطح ریشه در خلال Tippingدر شکل a و در حرکت انتقالی در شکل b مشاهده می‌شود. در خلال Tippingامکان تحلیل غیر مستقیم استخوان آلوئول به علت تجمع نیروها در نواحی کوچک، زیاد است. بنابراین نیرو بایستی تا حد امکان کم باشد.

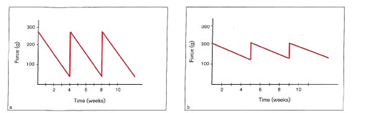
شکل 8-1. شکل a کاهش نیرو در طول زمان در فنری با میزان زیاد load/deflection و شکل b با میزان load/deflection کم را نشان می‌دهد. با در نظر گرفتن زمان یکسان 4 هفته، کاهش نیرو در فنری با load/deflection زیاد برابر 225 گرم و در فنری با load/deflection کم برابر 75 گرم است.

نیروهای مداوم

نیروی مداوم را می‌توان توسط وایرهایی با کم و با دامنه کاری مناسب به دست آورد. در مرحله Leveling، هنگامیکه بین دندانها اختلاف قابل توجهی از نظر Level وجود دارد، به منظور حفظ انکوریج و افزایش فاصله بین ویزیتهای بیمار استفاده از این نوع وایرها توصیه می‌شود. نیروی به مقدار جزیی کاهش می‌یابد ولی هرگز در خلال بین 2 ویزیت که به طور کلینیکی 1 ماه است به صفر نمی‌رسد و بدین ترتیب منجر به حرکت کنترل شده و با ثبات دندانی می‌گردد (شکل a 9-1). نیروی ایجاد شده توسط فنر Open Coil با آلیاژ نیکل تیتانیوم یک نیروی پیوسته است.

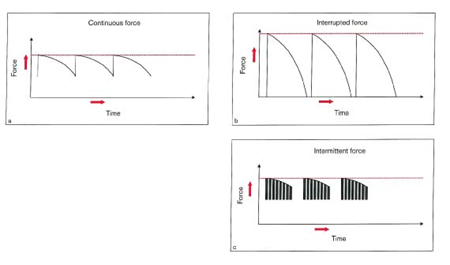
شکل 9-1. اثرات نیروی پیوسته در شکل a و نیروی Interrupted در شکل b و نیروی Intermittent در شکل c بر روی بافت پریودنتال نشان داده شده است.

نیروی Interrupted

نیروی Interrupted نیرویی است که بعد از مدت کوتاهی که اعمال می‌گردد به صفر می‌رسد. اگر در ابتدا نیروی به کار برده شده کم باشد دندان به مقدار جزیی توسط Direct Resorption حرکت می‌کند و سپس به موقعیت اولیه خود بر می‌گردد و سپس مجددا نیرو اعمال می‌شود. بعد از کاربرد نیروی Interrupted بافت‌های نگه دارنده دندان وارد مرحله ترمیم می‌شوند تا اینکه دوباره نیرو وارد گردد (شکل b 9-1).

بهترین مثال برای نیروی Interrupted استفاده از دستگاه Rapid Expansion می‌باشد.

نیروی Intermittent

نیروی Inrtermittent نیرویی است که با برداشتن دستگاه به صفر می‌رسد (شکل c 9-1). وقتی دستگاه مجددا به بیمار داده می‌شود، نیرو به مقداری که قبلا دستگاه در دهان بوده است می‌رسد و سپس بتدریج کاهش می‌یابد. دستگاه‌های خارج دهانی مثالی از نیروی Intermittent می‌باشد.

مرکز مقاومت

نقطه‌ای را که برآیند نیرو با محور طولی دندان قطع می‌کند و منجر به حرکت دندان می‌شود به عنوان مرکز مقاومت دندان نام گذاری می‌کنند. از نظر تئوری مرکز مقاومت یک دندان در ریشه قرار دارد و محل آن به سختی مشخص می‌گردد. مطالعات نشان داده است که مرکز مقاومت یک دندان تک ریشه در محور طولی ریشه و تقریباً در 24٪ تا 35٪ فاصله از لبه کرست آلوئول واقع شده است.

در بسیاری موارد مرکز مقاومت با مرکز ثقل Center of Mass به اشتباه گرفته می‌شود. مرکز ثقل عبارت است از نقطه تعادل یک جسم که تحت تاثیر نیروی جاذبه می‌باشد. در حالیکه دندان جسمی است که توسط ساختمانهای پریودنتال، استخوان و نیروی عضلات مهار شده است. بنابراین مرکز مقاومت، همان نقطه تعادل در اجسام مهار شده ‌است.

مرکز مقاومت برای هر دندانی مختص آن دندان می‌باشد. محل مرکز مقاومت بستگی به تعداد ریشه‌ها، میزان استخوان آلوئول و طول و مرفولوژی ریشه‌ها دارد. بنابراین مرکز مقاومت با تحلیل ریشه یا از بین رفتن استخوان به علت مشکلات پریودنتال تغییر می‌کند (شکل 10-1). در مواردی که استخوان آلوئول تحلیل می‌رود مرکز مقاومت به سمت اپیکال حرکت می‌کند.

مرکز چرخش

مرکز چرخش نقطه‌ای است که دندان اطراف آن نقطه می‌چرخد. موقعیت این نقطه به سیستم نیرویی که به آن وارد می‌شود مثل نسبت وابسته است. وقتی یک زوج نیرو به دندان وارد می‌شود این نقطه بر روی مرکز مقاومت منطبق می‌شود به عبارت دیگر دندان در اطراف مرکز مقاومت می‌چرخد. در حرکت انتقالی مرکز چرخش در بی نهایت قرار دارد که بدین معنی است که چرخشی وجود ندارد. این موضوع با جزئیات بیشتری در قسمت در این فصل توضیح داده خواهد شد.

گشتاور

گشتاور در اثر نیرو ایجاد می‌شود و باعث چرخش یا Tipping دندان می‌گردد. گشتاور توسط ضرب نیرو (F) در فاصله عمودی بین مرکز مقاومت و محلی که نیرو اعمال می‌شود d ×M=F مشخص می‌گردد (شکل 11-1) و در ارتودنسی با واحد گرم × میلیمتر (gr × mm) اندازه‌‌گیری می‌شود.

نیروهایی که از مرکز مقاومت عبور می‌کنند، به علت اینکه فاصله تا مرکز مقاومت صفر است، گشتاور ایجاد نمی‌کنند. بنابراین دندان نمی‌چرخد و فقط حرکت انتقالی خواهد داشت (شکل 12-1). از آنجائیکه گشتاور هم به نیرو و هم به فاصله‌ای که نیرو تا مرکز مقاومت اعمال می‌شود وابسته است می‌توان با دو برابر کردن فاصله و نصف کردن نیرو و یا برعکس اثر چرخشی یکسانی را به دست آورد. در مواردی که نیرو زیاد نیست، اما فاصله‌ایی که نیرو تا مرکز مقاومت دارد زیاد است به علت گشتاور زیاد ممکن است به بافت‌های پریودنتال آسیب وارد شود.

نیروی مزدوج

نیروی مزدوج سیستمی است که دارای 2 نیروی موازی در خلاف جهت با مقدار مساوی می‌باشد. هر نقطه‌ای از جسم که نیروی مزدوج به آن وارد شود تحت تاثیر حرکت چرخشی در همان مسیر و با همان مقدار نیرو قرار می‌گیرد. محلی که نیروی مزدوج وارد می‌شود، مهم نیست، جسم حول مرکز مقاومت می‌چرخد. به عبارت دیگر مرکز مقاومت و مرکز چرخش روی هم قرار می‌گیرند (شکل 13-1). برای مثال وقتی Torque یا (Third- Order Couple) به داخل براکت دندان انسیزور وارد شود باعث Tippingدندان حول مرکز مقاومت آن می‌شود. این پدیده با جزئیات بیشتر در قسمت سیستم‌های نیروی مساوی در این فصل توضیح داده شده است. مقدار گشتاور با حاصل ضرب مقدار یکی از نیروها در فاصله عمودی بین راستای دو نیرو به دست می‌آید.

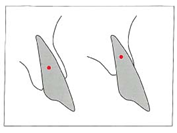
شکل 10-1. مرکز مقاومت به علت تحلیل استخوان آلوئول یا بافت‌های نگه دارنده دندان به سمت اپیکال حرکت می‌کند.

شکل 11-1. راستای نیرویی که به دندان وارد می‌شود از مرکز مقاومت دندان نمی‌گذرد و باعث ایجاد گشتاور می‌شود که تولید حرکت چرخشی Tippingبر روی دندان می‌نماید. براساس فرمول D × F = M گشتاور با حاصلضرب مقدار نیرو در فاصله عمودی از راستایی که نیرو وارد می‌شود تا مرکز مقاومت به دست می‌آید.

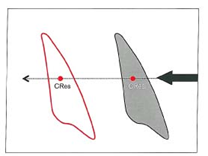
شکل 12-1. وقتی نیرو از مرکز مقاومت دندان می‌گذرد باعث حرکت انتقالی می‌شود. در حرکت انتقالی مرکز مقاومت در راستای نیرویی که به آن وارد می‌شود قرار می‌گیرد.

 

 

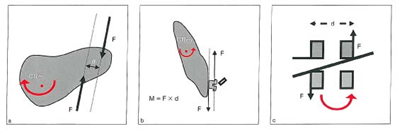
شکل 13-1. نیروی مزدوج باعث حرکت چرخشی در اطراف مرکز مقاومت یک جسم بدون توجه به نقطه‌ای که نیرو وارد می‌شود، می‌گردد. بدین ترتیب مرکز چرخش و مرکز مقاومت روی هم قرار دارند (a). در اینجا 2 مثال از نیروی مزدوج در دستگاه ثابت نشان داده شده است در شکل b نیروی (Third Order) Torque و در شکل c کاربرد Antitip (Second Order) مشاهده می‌شود. برای محاسبه گشتاور کافی است که مقدار یکی از نیروها (F) در فاصله عمودی بین راستای 2 نیرو (D) ضرب گردد.

انتقال نیرو در امتداد راستای نیرو

نیرو می‌تواند بدون هیچ گونه تغییری در خصوصیات فیزیکی در امتداد راستای خود انتقال یابد. به شرطی که راستای نیرو تغییر نکند، هر نوع نیرویی که بر دندان اعمال می‌گردد چه از طریق Open Coil Spring و یا از طریق Chain Elastic دندان را به عقب بکشد، دارای اثر یکسانی می باشد. اصول انتقال نیرو این نکته را شرح می‌دهد که اثر نیرو بر روی دندان به راستای نیرو وابسته نیست.

تعادل سکون و آنالیز اجسام آزاد

قوانین تعادل سکون به طور مشابه‌ای برای هر شیئی و هر قسمتی از آن و برای هر سیستم مکانیکی و هر قسمتی از آن به کار برده می‌شود. بنابراین به منظور درک آسان نیروی های وارد شده بر روی سیستم‌های مکانیکی فقط کافی است که قسمتی از سیستم مکانیکی را در یک شیئی آزاد آنالیز نمائیم. برای مثال به منظور روشن کردن آثار نیروها در قوس فکی کافی است که رابطه بین 2 دندان را بجای رابطه بین 14 دندان آنالیز نمائیم. بدیهی است که نیروهای وارد شده در این سیستم دو دندانی بایستی در تعادل باشند. به طور خلاصه آنالیز نیروها در قسمت کوچکی از یک شیء آزاد و یا آنالیز یک شیء در حال سکون باعث می‌شود که متخصص ارتودنسی بتواند راجع به کل سیستم ایده مناسبی داشته باشد.

علم استاتیک به تعادل اجسام تحت اثر نیروها می‌پردازد. قانون اصلی استاتیک قانون اول نیوتن است که می‌گوید اگر جسمی در حال سکون و یا دارای حرکت ثابت در مسیر خاصی است برآیند نیروها که بر این جسم اثر می‌کنند برابر صفر است. به عبارت دیگر، قانون تعادل سکون می‌گوید که در هر نقطه‌ای از جسم جمع جبری نیروها بایستی صفر باشد .

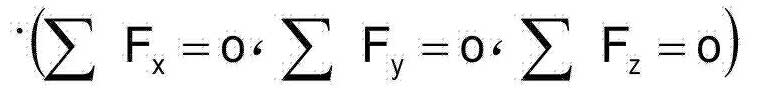
در جسمی که در موقعیت چرخشی بالانس شده قرار دارد جمع جبری تمام گشتاورها بایستی صفر باشد .

مجموع گشتاورها برای هر قسمتی از جسم که در تعادل سکون قرار دارد برابر صفر است. در این خصوص به شکل 14-1 مراجعه شود. درک این قانون بسیار مهم است زیرا پایه و اساس کاربردهای کلینیکی در درمانهای ارتودنسی است.

کتابی که در شکل 15-1 مشاهده می‌شود در حالت تعادل است. عاملی که باعث می‌شود این کتاب در حالت تعادل بماند نیروی ناشی از وزن کتاب است که در شکل با A نشان داده شده است. وزن کتاب بر روی میز نیرویی برابر و در خلاف جهت ایجاد می‌کند که در شکل با N نشان داده شده است. چون سیستم در حالت تعادل است، نیروهایی که بر جسم اثر می‌کند در حالت تعادل می‌باشند. بهترین شرایط برای یک جسم در حال تعادل این است که هیچ حرکتی در سیستم نباشد.

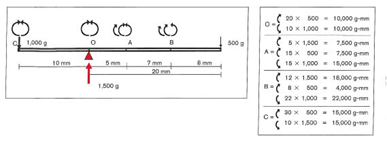
شکل 14-1. در تعادل سکون مقدار گشتاورها در اطراف هر نقطه باید برابر باشند. جمع جبری گشتاور نیروها در خلاف جهت عقربه‌های ساعت و در جهت عقربه‌های ساعت در نقاط O،‌ A ، B، C بایستی صفر باشند.

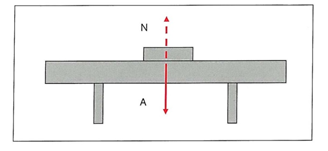
شکل 15-1. کتاب در روی میز در حالت تعادل قرار دارد. برای اینکه کتاب در تعادل بالانس باقی بماند نیروی مخالف وزن کتاب که در اینجا با N نشان داده شده است باید با نیروی وزن کتاب که با A نشان داده شده است مساوی و در خلاف جهت آن باشد.

حرکت دندان

حرکت Tipping

حرکت Tipping کنترل شده و کنترل نشده

حرکت Tipping ساده ترین نوع حرکت دندانی است. وقتی یک نیروی منفرد توسط سیم با مقطع گرد در براکت اعمال می‌گردد، دندان حول مرکز چرخش که در وسط ریشه و نزدیک مرکز مقاومت است، ‌می‌چرخد. این نیروی منفرد باعث حرکت تاج و ریشه در خلاف جهت می‌شود. این حرکت که توسط گشتاور نیرو (M1) ایجاد می‌شود نیروی Tipping کنترل نشده نام دارد (شکل a16-1) که از نظر کلینیکی نامطلوب است. در این حرکت، نسبت از تقریبا به می‌تواند تغییر کند (به قسمت گشتاور به نیرو در همین فصل مراجعه شود).

اگر گشتاور در خلاف جهت عقربه‌های ساعت (M2=Torque) توسط سیم با مقطع مربع مستطیل به نیروی قبلی اضافه گردد دندان به سمت دیستال Tip می‌شود که حرکت Tipping کنترل شده نامیده می‌شود. این حرکت از نظر کلینیکی مطلوب است. در این حرکت، مرکز چرخش به سمت آپکس حرکت می‌کند و دندان حول دایره‌ای به شعاع بزرگتر می‌چرخد. در حرکت Tipping کنترل شده نسبت از به تغییر می‌کند.

وقتی گشتاوری در خلاف جهت عقربه‌های ساعت (M2, Torque) اعمال گردد و مقدار آن مساوی با گشتاوری باشد که توسط نیروی اولیه ایجاد شده است (M1)، دو گشتاور همدیگر را خنثی می‌کنند و چرخشی ایجاد نمی‌شود. در این حالت، ‌مرکز چرخش وجود ندارد (مرکز چرخش در بی نهایت است) و دندان حرکت انتقالی یا Bodily می‌یابد (شکل C16-1). در حرکت انتقالی نسبت تقریبا برابر تا است. از نظر کلینیکی حرکت انتقالی یک حرکت مطلوب است اما ایجاد این حرکت و نگه‌داری از آن مشکل است. اگر گشتاور در خلاف جهت عقربه‌های ساعت (M2, Torque) افزایش یابد به طوری که نسبت تقریبا به برسد در آن موقع گشتاور ایجاد شده از گشتاور M1 بیشتر می‌شود و در این صورت ریشه دندان حرکت می‌کند و مرکز چرخش در تاج واقع می‌شود (شکل d16-1).

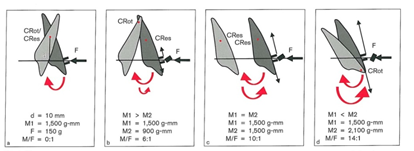
شکل 16-1. تغییر در نسبت باعث تغییر موقعیت مرکز چرخش می‌شود. در حرکت Tippingکنترل نشده نسبت برابر است و مرکز چرخش بسیار نزدیک به مرکز مقاومت است. (a). در حالیکه در حرکت Tipping کنترل شده نسبت برابر است و مرکز چرخش نزدیک به آپکس قرار می‌گیرد (b). در حرکت انتقالی نسبت برابر است و مرکز چرخش در بی‌نهایت قرار دارد به عبارت دیگر چرخشی وجود ندارد. در حرکت ریشه نسبت برابر است و مرکز چرخش در لبه تاج قرار دارد.

حرکت انتقالی

از نظر تئوری حرکت انتقالی بدون هیچ گونه تغییر در زاویه جسم نسبت به مرجعی مشخص می‌باشد (شکل 12-1). در خلال حرکت انتقالی همه نقاط یک جسم در فاصله یکسانی نسبت به همدیگر حرکت می‌کنند و بدین ترتیب همه نقاط دارای سرعت یکسانی می‌باشند.

حرکت چرخشی

حرکت چرخشی، حرکت جسم با تغییر زاویه نسبت به یک مرجع مشخص می‌باشد. اگر جسم حول مرکز مقاومت چرخش نماید، به آن حرکت چرخشی مطلق Pure Rotation گفته می‌شود.

سیستم‌های تعادل نیرو

همانگونه که قبلا ذکر شد این امکان وجود دارد که نیروها را بتوان در امتداد راستای خود بدون تغییر در خصوصیات فیزیکی آنها منتقل کرد. ولی امکان انتقال نیروها به موازات جهت وارد شدن نیروها وجود ندارد زیرا با تغییر محل اعمال نیرو، فاصله نسبت به مرکز مقاومت تغییر می کند بنابراین نوع حرکت دندانی عوض می شود (شکل‌های 11-1 و 12-1). اصول تعادل نیرو در شکل 17-1 مشاهده می‌شود و بیان می‌‌کند که همان حرکت انتقالی که با عبور نیرو از مرکز مقاومت دندان ایجاد می‌شود می‌تواند با عبور نیرو از داخل براکت هم ایجاد شود. نیروهایی که از مرکز مقاومت عبور می‌کنند باعث حرکت انتقالی می‌شوند. از نظر کلینیکی به علت محدودیت‌های اناتومیکی و بیومکانیکی همیشه این امکان وجود ندارد که بتوان نیرو را از مرکز مقاومت دندان عبور داد (سیستم 1). بنابراین این سیستم باید توسط سیستم دیگری که در آن نیرو از تاج می‌گذرد جایگزین شود (سیستم 2). نیروهایی که از تاج عبور داده می‌شوند، همیشه از مرکز مقاومت عبور نمی‌کنند. این نیروها باعث چرخش (Tipping) دندانها به علت وجود گشتاور در جهت عقربه‌های ساعت میشوند (M1). برای ایجاد حرکت انتقالی این گشتاور بایستی با گشتاور دیگری (M2) که برابر و در جهت مخالف باشد در تعادل قرار گیرد به عبارت دیگر همانگونه که در شکل 17-1 مشاهده میشود باید gr/mm 1500 = M1 = M2باشد. در این مثال M2 می‌تواند با اعمال نیرو در داخل براکت انسیزور یا Palatal Root Torque ایجاد شود (شکل c17-1). در نتیجه گشتاورها همدیگر را خنثی می‌کنند و فقط نیروی 150 گرم باقی می‌ماند که باعث حرکت انتقالی می‌شود.

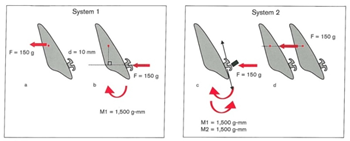
شکل 17-1.a) ) از آنجائیکه حرکت انتقالی توسط نیرویی که از داخل مرکز مقاومت یک دندان می‌گذرد عملی نیست، این حرکت می‌تواند با اعمال نیرو در سیستم دیگری که از تاج می‌گذرد ایجاد شود. (b) وقتی نیروی 150 گرمی اعمال می‌شود گشتاور (M1) در جهت عقربه‌های ساعت به وجود می‌آید که برابر با gr × mm 1500 می‌باشد. (c) اگر این گشتاور با گشتاور دیگری (M2) که از نظر مقدار برابر ولی در خلاف جهت می‌باشد خنثی گردد تنها نیروی 150 گرمی باقی می‌ماند. (d) اگر این نیرو در تاج اعمال شود باعث حرکت انتقالی می‌شود و مثل این می‌ماند که نیرو در مرکز مقاومت اعمال شود.

نسبت گشتاور به نیرو

دانستن نسبت برای کنترل حرکت دندانی لازم است (شکل 16-1). نسبت تعیین کننده نوع حرکت دندانی یا محل مرکز چرخش است. براساس فرمول نسبت همان فاصله است . همانگونه که فاصله بین مرکز مقاومت و محل اعمال نیرو بیشتر می‌شود مقدار هم افزایش می‌یابد. در مثال شکل a16-1 نیروی دیستالی 150 گرم به براکت اعمال می‌گردد. از آنجایکه نیرو از مرکز مقاومت نمی‌گذرد mm10 = d و گشتاور مخالف (M2) بر روی براکت اعمال نشده است مقدار برابر است (گشتاور دوم وجود ندارد). دندان حول مرکز چرخش که در اطراف ریشه و نزدیک به مرکز مقاومت است می‌چرخد. وقتی تاج به سمت دیستال و آپکس به سمت مزیال حرکت کند حرکت Tipping کنترل نشده ایجاد میشود. از نظر کلینیکی Tipping ساده‌ترین نوع حرکت است. فنرها و پیچ‌ها در دستگاه‌های متحرک حرکت Tipping کنترل نشده به وجود می‌آورند. زیرا در این دستگاه‌ها فقط یک نیروی منفرد است که به دندان وارد می‌شود و هیچ گونه اتچمنتی روی دندان برای ایجاد گشتاور مخالف وجود ندارد (شکل 11-1). به همین ترتیب در سیستم Begg نیز حرکت مشابه حرکت ذکر شده در اطراف سیم‌های گرد ایجاد می‌گردد.

اگر گشتاوری در خلاف جهت عقربه‌های ساعت (M2) به میزان 900 گرم در میلیمتر برای Palatal Root Torque ایجاد شود مقدار برابر خواهد شد (شکل b16-1). در این حالت مرکز چرخش به سمت آپکس حرکت می‌کند به طوری که دندان به صورت پاندول در اطراف آپکس (یا یک نقطه در نزدیک آن) حرکت می‌کند. این حرکت یک حرکت Tipping کنترل شده است.

اگر گشتاور M2 به مقدار 1500 گرم در میلیمتر افزایش یابد در آن موقع نسبت برابر می‌شود. گشتاورها همدیگر را خنثی می‌کنند و فقط 150 گرم نیرو باقی می‌ماند که باعث حرکت انتقالی می‌شود. در این حالت مرکز چرخش دندانها در بی‌نهایت قرار می‌گیرد (شکل c16-1). اگر مقدار گشتاور M2 باز هم افزایش یابد و به میزان 2100 گرم در میلیمتر برسد نسبت برابر خواهد شد در این موقع مرکز چرخش در تاج قرار می‌گیرد (شکل d16-1).

مطالب ذکر شده در بعد عرضی هم معتبر می‌باشند. عقب بردن کانین با وایر Segmented که از مرکز مقاومت دور باشد باعث حرکت چرخشی دیستولینگوال کانین می‌شود این چرخش را می توان با Antirotation Bend تصحیح کرد. در بعد عرضی نسبت برابر فاصله بین مرکز مقاومت و محل اعمال نیرو است (شکل 18-1).

با اعمال نیروی دیستال گشتاوری ایجاد می‌شود که کانین به سمت دیستال Tip می‌شود. این گشتاور با Antitip Bend (گشتاور در خلاف جهت عقربه‌های ساعت) خنثی می‌گردد. مقدار این گشتاور وابسته به مقدار Bend و عرض براکت است. توجه داشته باشید که برای به وجود آوردن میزان گشتاور مساوی، نیرویی که بر روی براکتهای کم عرض اعمال می‌شود باید از نیرویی که بر روی براکت‌های پهن در Second Order Bend اعمال می‌شود، بیشتر باشد. این اختلاف به علت فاصله‌های متفاوت است. هر چه فاصله بیشتر باشد نیروی کمتری لازم است و هر چه فاصله کمتر باشد نیروی بیشتری لازم است. چون فاصله Wingها در براکت‌های کم عرض کمتر از براکتهای پهن است میزان نیرو بیشتر خواهد بود. برای مثال اگر فرض شود که عرض براکت ها برابر 4/3 میلیمتر باشد (d) میزان نیروی اعمال شده در براکت می‌تواند به طریق زیر محاسبه شود:

اگر براکت کم عرض (2 میلیمتر) به کار برده شود میزان نیروی موثر در Wing براکت برابر 750 گرم خواهد بود در خلال کاربرد (Torque) Third Order Bend به علت اینکه فاصله در بین Wing‌ها کم است مقدار نیرو در بین Wing براکت بیشتر خواهد بود (شکل c19-1). این مورد یکی از دلایلی است که Wingهای براکت های سرامیکی در هنگام عمل Torque می‌شکنند.

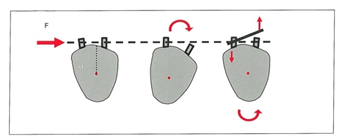
شکل 18-1. نوع حرکت دندانی در مقطع ساژیتال که در شکل 17-1 مشاهده می‌شود در مقطع عرضی نیز صادق است. تنها اختلاف این است که یک زوج نیرو (Antirotation) در خم First Order به کار برده می‌شود. D = فاصله. F= نیرو.

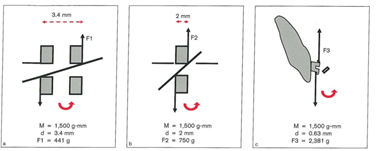
شکل 19-1. برای ایجاد گشتاور مساوی (M)، نیروی وارد شده به Wingهای براکت با افزایش عرض بین Wingها کاهش می‌یابد. از آنجائیکه فاصله بین Wingها در براکت‌های پهن (4/3 میلیمتر) (a) زیادتر از براکتهای کم عرض (2 میلیمتر) (b) است نیرو در براکت‌های پهن کمتر از کم عرض می‌باشد. در حرکت Torque میزان نیرو در Wing‌های براکت بسیار زیاد است چون فاصله (63/0 میلیمتر) (c) بسیار کم است.

نسبت گشتاور به دندان با از تحلیل استخوان آلوئول

مرکز چرخش دندان به طول، مقدار و مرفولوژی ریشه‌ها و به میزان ساپورت استخوان آلوئول وابسته است. در تحلیل ریشه و یا کوتاه بودن ریشه‌ها مرکز مقاومت به سمت آکلوزال حرکت می‌کند. اما در موقعی که استخوان آلوئول تحلیل یابد مرکز مقاومت به سمت آپکس حرکت می‌کند (شکل 20-1 و 10-1). این مطلب بخصوص در درمان بیماران بالغ که دارای مشکلات پریودنتال هستند، مهم است. همانگونه که فاصله بین براکت و مرکز مقاومت افزایش می‌یابد. نسبت زیاد می‌شود. برای به دست آوردن نسبت دو نکته باید مورد توجه قرار گیرد:

مورد اول این است که براکتها با تمایل به سمت ژنژیوال قرار گیرند. با قرار دادن براکتها به سمت ژنژیوال، سطح براکت به خوبی با دندان تطابق نخواهد داشت. بعلاوه قرار دادن Straight Wire به منظور Leveling مشکل خواهد بود. در اینصورت ممکن است لازم باشد که سیم دارای Step-Up باشد و این موضوع ممکن است بر روی Alignment تاثیر بگذارد.

مورد دیگر این است که گشتاور زیاد و یا نیرو کاهش یابد و یا ترکیبی از هر دو انجام شود. از نظر کلینیکی اگر وایر Segmented به کار برده شود، گشتاور قابل پیش بینی است. گشتاوری که توسط Antitip یا Torque ایجاد شود به طور دقیق قابل اندازه گیری نیست. بنابراین محاسبه نسبت با تغییر گشتاور بسیار مشکل است. به نظر می‌رسد که محاسبه مقدار نیرو براساس نوع حرکت دندانی عملی تر باشد.

Braun و همکاران نسبت را براساس موقعیت مرکز مقاومت ارزیابی نمودند. آنها ضریب گشتاور و هم چنین مقدار نیروهایی را که می‌بایست در مواردی که استخوان آلوئول دچار تحلیل می‌شوند را گزارش کردند (جدول 1-1).

از نقطه نظر کلینیکی تعیین مرکز مقاومت و مقدار دقیق و ثابت نگه داشتن این مقدار در خلال حرکت دندان بسیار مشکل است. Tanne و همکاران گزارش کردند که با تغییر بسیار کوچکی در نسبت و با وجود رابطه بین مرکز چرخش دندان و این نسبت، مرکز چرخش به میزان زیادی تغییر می‌کند. میزان نیرو یک فاکتور کلیدی در کنترل نسبت (حرکت دندان) است. اگر در اثر یک Loop بسیار فعال شده‌ حرکت Tipping غیر مطلوب ایجاد شود متخصص ارتودنسی باید اجازه دهد که سیم تا کامل شدن شدن حرکت ریشه،‌به فعالیت خود ادامه دهد.

اثر شکل Loop بر روی نسبت

کاهش (افزایش انعطاف پذیری) یکی از اهداف Loop است. بدین ترتیب می‌توان نیرو را در یک دامنه وسیع تری در محدوده خصوصیات فیزیولوژیک وارد نمود. Loop ها به علت داشتن خصوصیات فنری برای بستن فضا با طراحی‌های مختلف مکانیکی به کار برده می‌شوند. در خلال بستن فضا مهم است که حرکات دندانی در سگمنتهای قدام و خلف تحت کنترل باشند. حرکت Tipping کنترل نشده به علت عوارضی مثل از دست رفتن انکوریج و تحلیل ریشه که ممکن است در خلال Uprighting انجام شود، نامطلوب است. برای مثال با سیستم Begg فضای دندان در آورده شده در زمانی کوتاهی در دندانهای قدامی توسط حرکتTipping کنترل نشده با استفاده از وایر گرد و الاستیکهای C1 II قابل انجام است. لازم به ذکر است Uprighting دندانهای انسیزور به شدت tip شده،‌ نیاز به زمان طولانی و حفظ انکوریج دارد.

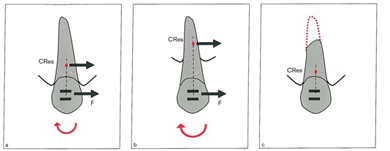
شکل 20-1. در بیماری که دچار تحلیل استخوان آلوئول شده است (u) مرکز مقاومت به سمت آبیکال حرکت می‌کند. بدین ترتیب فاصله (d) افزایش می‌یابد. (b). برای حرکت انتقالی نسبت باید افزایش یابد. از نظر کلینیکی بهتر است که نیرو (F) برای کنترل حرکت دندانی کاهش یابد. این موضوع بخصوص در افراد بالغی که دچار تحلیل استخوان آلوئول هستند و مشکلات پریودنتال دارند بسیار مهم است. در بیمارانی که تحلیل ریشه دارند (c) مرکز مقاومت به سمت اکلوزال حرکت می‌نماید.

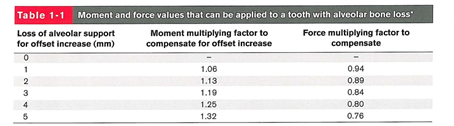
جدول 1-1. میزان نیرو و گشتاوری که می‌تواند در دندانی که دچار تحلیل ریشه است اعمال کرد.

شکل Loop اثر قابل توجهی بر روی نسبت دارد. مطالعات نشان داده است که نسبت در Vertical Loop برابر است. افزایش طول Loop نسبت را می‌تواند به افزایش دهد. افزایش ارتفاع در Loop به علت اینکه ممکن است به بافت‌های مخاطی صدمه بزند امکان پذیر نیست.

شکل 21-1 تغییرات نسبت در یک Vertical Loop با 6 میلیمتر ارتفاع و 20 درجه Anti Tip را نشان می‌دهد. توجه داشته باشید که با فعال نمودن یک میلیمتر Loop نسبت کمتر از است که باعث حرکت Tippingکنترل نشده می‌گردد. نسبت همانگونه که Loop غیر فعال می‌گردد افزایش می‌یابد. وقتی که Loop به مقدار 1/0 میلیمتر غیر فعال گردد نسبت به مقدار نزدیک می‌شود که باعث حرکت Tipping کنترل شده می‌گردد. وقتی Loop از 1/0 میلیمتر به صفر غیر فعال می‌گردد. نسبت تقریبا به مقدار افزایش می‌یابد.

پر واضح است که فعال شدن Loop به مقدار 1/0 میلیمتر از نظر کلینیکی قابل توجه است. کمترین خطا در فعال شدن Loop باعث تغییر مرکز چرخش به مقدار قابل توجهی می‌شود. از نقطه نظر کلینیکی در صورتی که دندان به مقدار یک میلیمتر فعال ‌شود، هنگام غیر فعال شدن 7/0 میلیمتر ابتدای آن دچار حرکت Tipping کنترل نشده خواهد شد (نسبت برابر ). مرکز چرخش به نقطه‌ای بین مرکز مقاومت و آپکس حرکت می‌کند. پس از آن دندان با فعال شدن Loop از 3/0 تا 12/0 میلیمتر حرکت Tipping کنترل شده خواهد داشت. نسبت به می رسد و مرکز چرخش به نقطه‌ای بین آپکس و بی‌نهایت منتقل می‌شود. همانگونه که Loop از 12/0 میلیمتر به 03/0 میلیمتر غیر فعال می‌گردد نسبت به نزدیک می‌شود و مرکز چرخش به سمت بی‌نهایت می‌رود و دندان حرکت انتقالی می‌یابد. با غیر فعال شدن Loop از 03/0 به صفر میلیمتر نسبت به مقدار افزایش می‌یابد و مرکز چرخش به سمت اکلوزال در تاج دندان نزدیک می‌شود در این حالت دندان حرکت ریشه خواهد داشت.

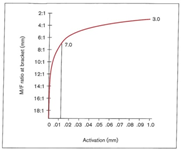
شکل 21-1. نسبت در Loop به ارتفاع 6 میلیمتر و Gable Bend به مقدار 20 درجه مشاهده می‌شود. در خلال غیر فعال شدن Loop به مقدار 9/0 میلیمتر نسبت به مقدار ثابتی باقی می‌ماند. سپس بطور قابل توجه‌ای تا افزایش می‌یابد.

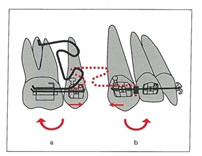
شکل 22-1. a موقعیت فعال شده و b موقعیت طبیعی T-Loop

میزان نیروی ایجاد شده در هر بار فعال شدن Loop‌های عمودی بسیار زیاد است. برای مثال نیروی ایجاد شده توسط Bull Loop با وایر استنلس استیل 0.025 × 0.018 اینچ تقریبا برابر 500 گرم می‌باشد. این نیروی زیاد باعث حرکت Tipping کنترل نشده و تحلیل ریشه می‌گردد. اگر فقط به 100 گرم نیاز باشد Loop می‌بایست فقط 2/0 میلیمتر فعال گردد که از نظر کلینیکی غیر عملی است. دو بازوی Loop بعد از فعال شدن سریعا بسته می‌شوند که باعث حرکت Tipping کنترل نشده می‌گردد. در صورت استفاده از وایر، دندان بتدریج با حرکت ریشه Upright می‌شود. مدت Uprighting به میزان Tipping و به نسبت وابسته است. هر چه دندان بیشتر Tip شود مدت زمان زیادتری برای Uprighting نیاز دارد.

از نقطه نظر کلینیکی Space Closing Loop مناسب می‌بایست به مقداری نسبت داشته باشد تا باعث حرکت Tipping کنترل شده گردد. مادامیکه Loop غیر فعال می‌گردد نسبت به طور افزایشی زیاد می‌گردد و باعث حرکت ریشه می‌شود. همانگونه که قبلا ذکر شد افزایش طول با اضافه کردن Helix به Loop باعث کم شدن میزان می‌شود. اما اثر مختصری روی دارد. به منظور افزایش نسبت توصیه می‌شود مقدار بیشتری سیم استفاده شود. به طور کلی طول سیم به 2 علت افزایش می‌یابد:

به منظور افزایش نسبت (در صورتیکه به صورت ژنژیوال قرار گیرد)
به منظور کاهش
فعال کردن بیشتر Loop–T ساخته شده از آلیاژ بتاتیتانیوم (B-Ti) و یا تیتانیوم مولیبدنیوم (TMA) مقدار بیشتری نسبت به Vertical Loop ایجاد می‌کند. بنابراین Loop-T می بایست قبل از قرار دادن بر روی براکت فعال شده باشد (شکل 22-1). گاهی اوقات Gabel Bend براساس نیاز بیمار می‌تواند تا 180 درجه از قبل فعال شده باشد. Loop-T ساخته شده از آلیاژ TMA به قطر 0.025 × 0.017 اینچ که به مقدار 180 درجه از قبل فعال شده باشد و سپس 7 میلیمتر به صورت افقی فعال گردد تقریباً 350 گرم نیرو ایجاد می‌کند. T-Loop ساخته شده از TMA با قطر 0.022 × 0.016 اینچ با همان Activation به میزان 243 گرم نیرو تولید می‌کند و لیکن وایر TMA با قطر .0250 × 0.017 و T-Loop به قطر 0.018 از جنس TMA کامپوزیتی ‌به میزان 333 گرم نیرو تولید می‌کند. برای ایجاد 150 گرم نیرو جهت عقب بردن کانین با T-Loop به قطر 0.022 × 0.016، نیاز به 4 میلیمتر فعال شدن می باشد.

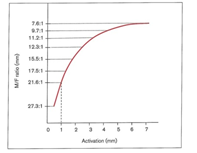
شکل 23-1 به دست آمده در T-Loop وایر TMA به قطر 0.022 × 0.016 را نشان می‌دهد. با فعال کردن 7 میلیمتر، نسبت به میزان خواهد رسید که باعث حرکت Tipping کنترل شده می‌گردد. میزان نیرو در هر واحد (یک میلیمتر) از فعال کردن Loop-T برابر 5/34 گرم خواهد بود که تقریبا مقدار کمی است. یک میلیمترخطا در فعال کردن Loop-T مقدار 5/34 گرم نیروی بیشتری به بافت‌های پریودنتال وارد می‌نماید.

همانگونه که Loop غیر فعال می‌گردد نسبت افزایش می‌یابد. وقتی Loop به میزان 7/2 میلیمتر غیر فعال گردد نسبت به میزان می‌رسد که باعث حرکت ریشه می‌گردد با غیر فعال شدن از 7/2 میلیمتر به 5/0 میلیمتر نسبت به مقدار می‌رسد.

شکل 23-1. به دست آمده توسط 7 میلی متر فعال کردن T-Loop وایر TMA 0.022 × 0.016 اینچ. به دست آمده توسط 1 میلی متر فعال کردن T-Loop تقریبا 7 برابر ( ) بیشتر از Vertical Loop ( ) می باشد. فعال کردن کامل (7 میلی متر) T-Loop به مقدار ایجاد می کند که باعث حرکت Tipping کنترل شده می گردد.

نتیجه

قوانین نیرو و حرکت فیزیک در ارتودنسی هم صادق است (مثل فشار، کشش، سختی، فنریت و حد کشسانی وایرها). تعاریفی همچون گشتاور، نیروی مزدوج، مرکز مقاومت، ‌مرکز چرخش، نسبت در کنترل حرکات دندانی نقش اساسی دارند. اصول فیزیکی که در کنار علم ارتودنسی وجود دارد باعث میشود که متخصص ارتودنسی بتواند طرح درمان و نوع دستگاه مورد نظر خود را برای رسیدن به نتایج مطلوب درمانی، مشخص نماید.

دانلود فصل اول از کتاب اصول علمی و کاربردی بیومکانیک در ارتودنسی(اصول فیزیکی) انتشارات جعفری